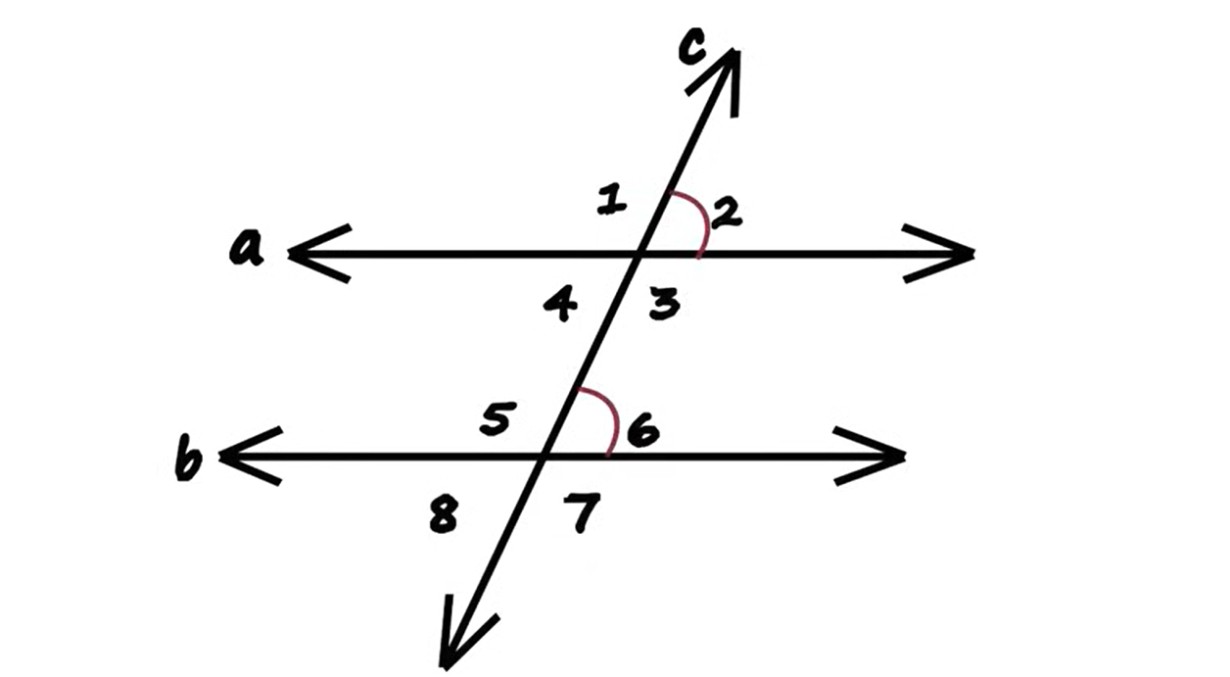
When I help students or even parents brushing up on geometry basics, one question comes up again and again: which diagram shows lines that must be parallel lines cut by a transversal? I used to overthink this myself until I realized it’s less about memorizing rules and more about spotting reliable patterns.
Once you train your eye to recognize a few key angle relationships, these questions stop feeling tricky. In my day-to-day routine of reviewing math concepts, I rely on quick visual checks rather than long calculations. That’s exactly what I’ll walk you through here—practical, repeatable habits you can use every time.
Why does a transversal reveal parallel lines so clearly?
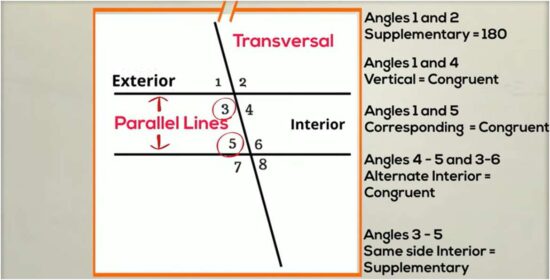
A transversal acts like a truth-teller. When it cuts across two lines, it creates angle pairs that either prove the lines run parallel or expose that they don’t.
I like to think of it as a stress test. Parallel lines respond in very specific, predictable ways. Non-parallel lines don’t. When you see certain angle relationships show up cleanly and consistently, the diagram basically confirms the answer for you without extra work.
This matters because many diagrams try to distract you with extra angles. I ignore most of them. I focus only on the relationships that geometry guarantees. That habit alone saves time and avoids careless mistakes.
How do corresponding angles prove lines are parallel?
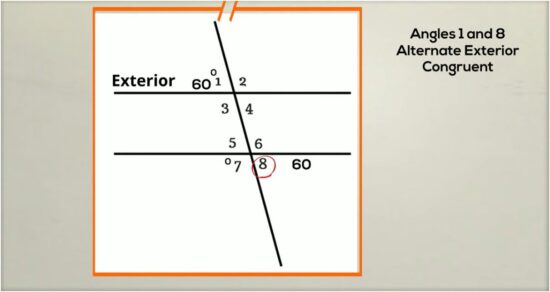
Corresponding angles are my first checkpoint. They’re easy to spot and easy to trust.
These angles sit in the same relative position at each intersection—top-right with top-right, bottom-left with bottom-left. When I see corresponding angles labeled with equal measures, I know immediately the lines must be parallel.
For example, if one intersection shows a top-right angle of 115° and the other intersection shows the same position labeled 115°, the case is closed. No extra steps needed. That diagram proves the lines are parallel by definition.
Why do alternate interior angles matter so much?
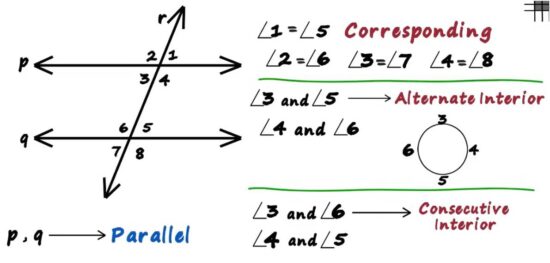
Alternate interior angles feel slightly more subtle, but once you spot them, they’re just as powerful.
These angles sit between the two lines and on opposite sides of the transversal. I picture a clean “Z” shape every time. If both angles match in measure, the lines cannot be anything other than parallel.
In practice, I pause and trace the Z with my finger or eyes. If the angles line up and the numbers match, I don’t second-guess it. Geometry gives us this rule for a reason—it always holds.
When do same-side interior angles confirm parallel lines?
Same-side interior angles don’t need to match. Instead, they need to cooperate.
These angles live between the two lines and sit on the same side of the transversal. When their measures add up to exactly 180°, the lines must be parallel. I visualize a “C” or “U” shape to spot them quickly.
If one angle shows 70° and the other shows 110°, I immediately check the sum. When it hits 180°, the diagram proves parallel lines without debate.
Which diagram shows lines that must be parallel lines cut by a transversal?
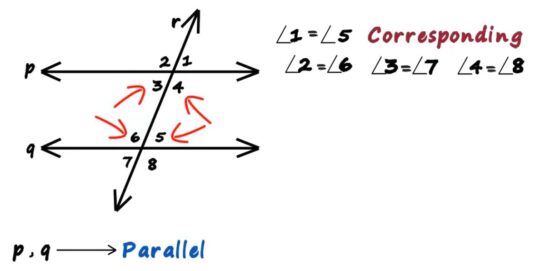
This is the core habit I use every time I answer which diagram shows lines that must be parallel lines cut by a transversal?
I don’t scan the whole diagram. I search for one solid proof:
- A matching pair of corresponding angles
- A matching pair of alternate interior angles
- A same-side interior pair that adds to 180°
If the diagram clearly labels one of these relationships, that’s the correct answer. Even a single qualifying angle pair locks it in.
If the diagram only shows random adjacent angles or values that don’t align with these rules, I move on immediately. Those diagrams don’t guarantee parallel lines.
How I quickly check diagrams without overthinking
This routine keeps me fast and accurate, especially on tests or homework reviews.
| Angle Pattern | What I Check | What It Proves |
| Corresponding | Same position, same measure | Lines are parallel |
| Alternate Interior | Z-shape, same measure | Lines are parallel |
| Same-Side Interior | C-shape, sum is 180° | Lines are parallel |
I glance at this mental table every time. It’s simple, repeatable, and stress-free.
How do I solve transversal diagram questions step by step?
When I teach this, I always recommend a fixed sequence so nothing slips through.
Step 1: Identify the transversal
I find the line that cuts across the others. Everything depends on this.
Step 2: Locate angle pairs
I look for corresponding, alternate interior, or same-side interior angles. I ignore everything else.
Step 3: Compare values
I check if angles match or add to 180°. I trust the math and move on.
Step 4: Confirm the conclusion
If one rule fits, the lines must be parallel. No extra justification needed.
This method keeps my answers consistent, even under time pressure.
FAQ: Real questions people ask about parallel lines and transversals
1. How many angle pairs do I need to prove lines are parallel?
Just one. A single pair of corresponding angles, alternate interior angles, or supplementary same-side interior angles is enough. You don’t need to prove all of them. Geometry only requires one valid relationship to confirm parallel lines.
2. What if the angles look close but don’t match exactly?
Then the diagram does not prove the lines are parallel. Geometry depends on exact relationships, not approximations. If the measures don’t clearly match or add to 180°, the lines might not be parallel.
3. Can alternate exterior angles also prove parallel lines?
Yes. Alternate exterior angles also work when they are equal. They follow the same logic as alternate interior angles, just outside the two lines instead of between them.
4. Why do test questions include extra angles?
They test focus. Extra angles distract you from the meaningful relationships. Once you train yourself to ignore irrelevant angles, these problems become much easier and faster to solve.
Parallel Lines Don’t Lie—You Just Need to Read Them Right
Every time I see which diagram shows lines that must be parallel lines cut by a transversal, I remind myself that the diagram already contains the answer. My job is simply to recognize it.
Once you build the habit of spotting the right angle relationships, these questions stop feeling like puzzles and start feeling automatic. That confidence carries over into harder geometry topics too.
My best tip? Trust the patterns. Geometry rewards consistency, and parallel lines always follow the same rules.
Disclaimer: All images used in this blog are for editorial and informational purposes only. The visuals are either AI-generated or sourced from Infinity Learn NEET and MooMooMath and Science. They do not represent actual events or endorse any specific brands or individuals. All trademarks, logos, and copyrighted materials belong to their respective owners.